Welcome to the start of your circular functions insight journey
The circular functions are extensions of the trigonometry functions that you know from right-angled triangles. Often, the word trigonometry is used for these more general functions, but I prefer to use the term "circular functions"— and you are about to find out why!
Take your time with each page. Work on the questions before moving to the answers!
Defining the circular functions
My idea is to start with the trigonometric functions that my students already know, namely, ratios of sides in right-angled triangles, and to give them the chance to see for themselves how to extend these functions to include all real numbers in their domains. The purpose here is to begin a long process of divorcing the trigonometric functions from right-angled triangles, and ultimately from angles altogether.
At the same time, I want to decouple the functions from calculators; that is, to remind students that the trigonometric functions are more than just something that your calculator gives you. To do this, I want my students to know the easy exact values of trigonometric functions. This has to do with embedding the image of the unit circle in the minds' eyes of my students, and with continually reinforcing the interpretation of the functions in terms of the unit circle, again in opposition to an understanding of the functions as something that the calculator tells you. This then means that the solution of trigonometric equations is built on a firm foundation.
Any text in blue and any diagrams with a blue border are only for you, and do not appear on the student version.
For you as a teacher, you can, if you feel attracted to the idea, use them to hand more responsibility for progress to your students, encouraging them always to think for themselves rather than to outsource their thinking to you, to their calculator, to the mark-scheme, or to artificial intelligence. This takes a tremendous amount of patience on your part: the patience to give them time to figure something out for themselves either individually or, more likely, by collaborating with each other.
These sheets are not in any way a complete course: they provide a context within which to develop insight and understanding by encouraging self-reliance and curiosity. They will not replace more traditional resources; in particular, you will need both routine exercises and more challenging sets of problems both for fluency and for creative problem-solving.
Work on the question in yellow. When you are ready, navigate to the next page using arrow keys, swiping, or hovering near the bottom of the page. Compare your work to the answer in green. Don't go to the answer too soon! Work your way through the whole document this way, but please don't get impatient — take your time!
First, let's think about the name for this topic. It's usually called "trigonometry". "Trigonon" is Greek for a three-sided shape while "metron" means measure, so "trigonometry" means "measurement of triangles". Here, however, we are moving on from triangles to something far more general. In a few minutes, you will see why the name "circular functions" makes far more sense.
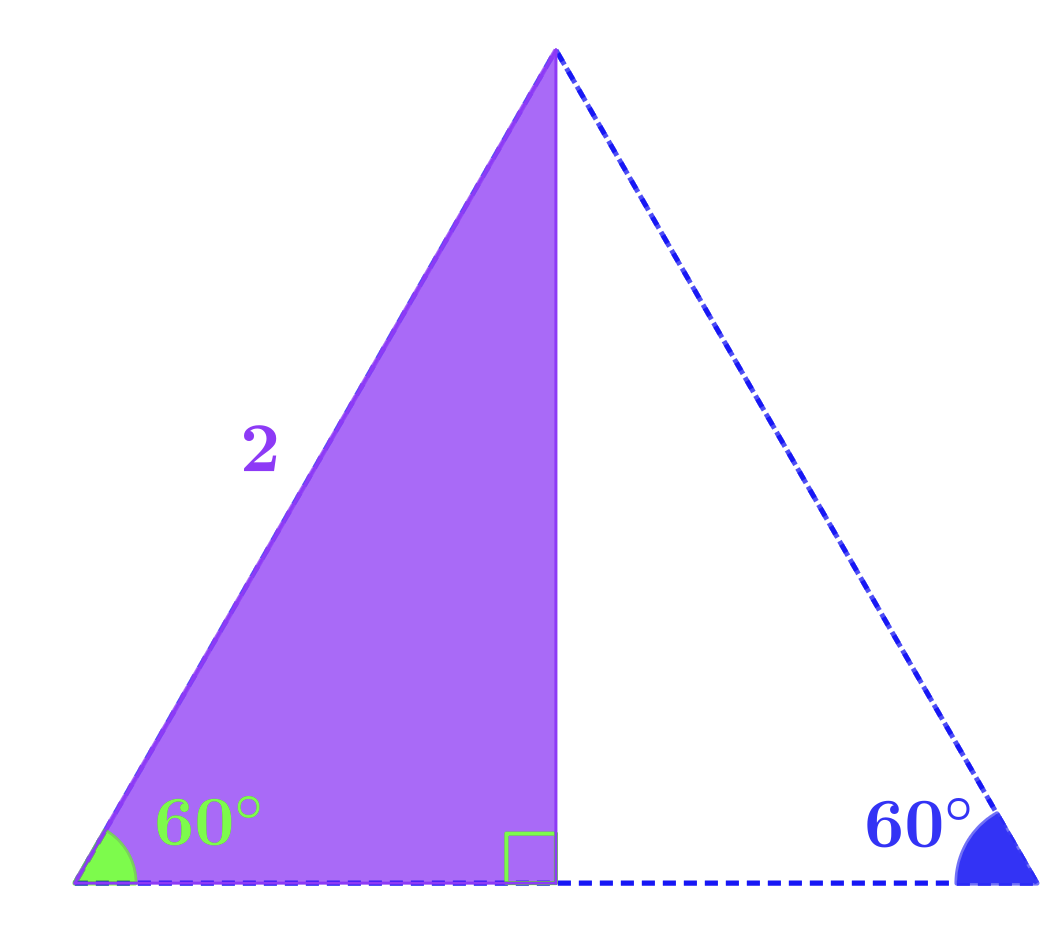
Use this diagram to find sin, cos, and tan of \(60°\) and \(30°\).
This is a perfect introduction to the idea that your students can work together to figure things out without your direct help. Collaboration is the key here: they help each other along both with ideas and with motivation. They can achieve so much more together than they can alone.
They have to figure out:
- that they need to know the sides of the right-angled triangle
- that the large triangle is equilateral and is divided exactly into two halves
- that they can use Pythagoras to find the height
- that they can then use the ratios that they already know to find the trig functions
and these are all steps they can take without the help of their teacher.
There is always a balance to find when deciding how much information to put in the question or diagram. I could have put the third \(60°\) angle in the diagram, for example, or included the fact that the triangle is equilateral in the "question". I could have left out the shading of the right-angled triangle and the vertical line segment, or even have left out the side-length of the equilateral triangle. The problem would still have been solvable, but this version seems to me to strike a good balance for a wide range of classes.
The temptation for the teacher will always be to help out, to give a hint, to answer a request for help, or to show them how to do it. Resisting this temptation takes considerable patience, sometimes in the face of strongly expressed frustration. But by giving your students the space to try out ideas, you allow them to gain greatly in terms of confidence in their own abilities, and to experience the satisfaction of having figured out something significant.
It is tremendously important that they tackle this page, and indeed most if not all of this lesson, without a calculator. I want them to be comfortable with exact values (rather than decimal approximations) and with fractions that include square roots. It is also important to me that they understand why, for example, \(\dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}\), and are able to use both forms later in calculations if necessary.
Use this diagram to find sin, cos, and tan of \(60°\) and \(30°\).
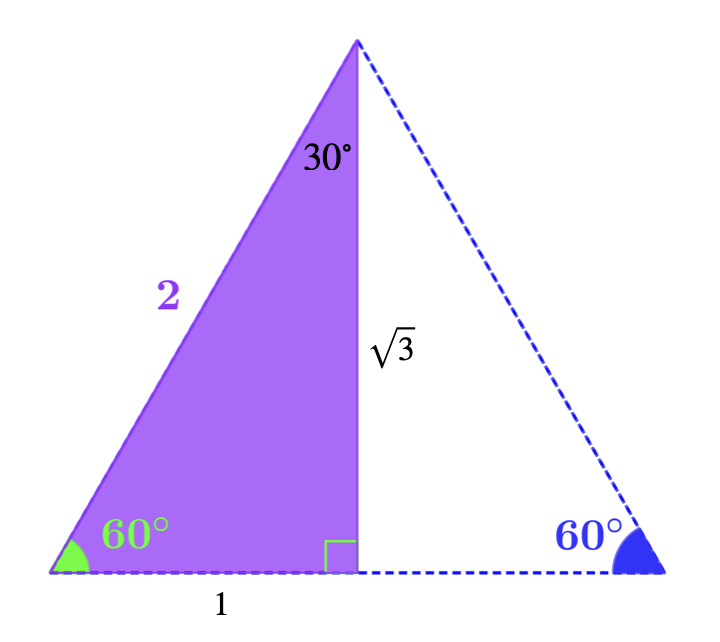
The big triangle is equilateral, so the base of the shaded triangle is half the length of the side of the big triangle. Then Pythagoras gives the height \(\sqrt{3}\) :
| \(\cos 60° = \dfrac{1}{2}\) | \(\sin 60° = \dfrac{\sqrt{3}}{2}\) | \(\tan 60° = \sqrt{3}\) |
| \(\sin 30° = \dfrac{1}{2}\) | \(\cos 30° = \dfrac{\sqrt{3}}{2}\) | \(\tan 30° = \dfrac{1}{\sqrt{3}} = \dfrac{\sqrt{3}}{3}\) |
Use this diagram to find sin, cos, and tan of \(45°\).
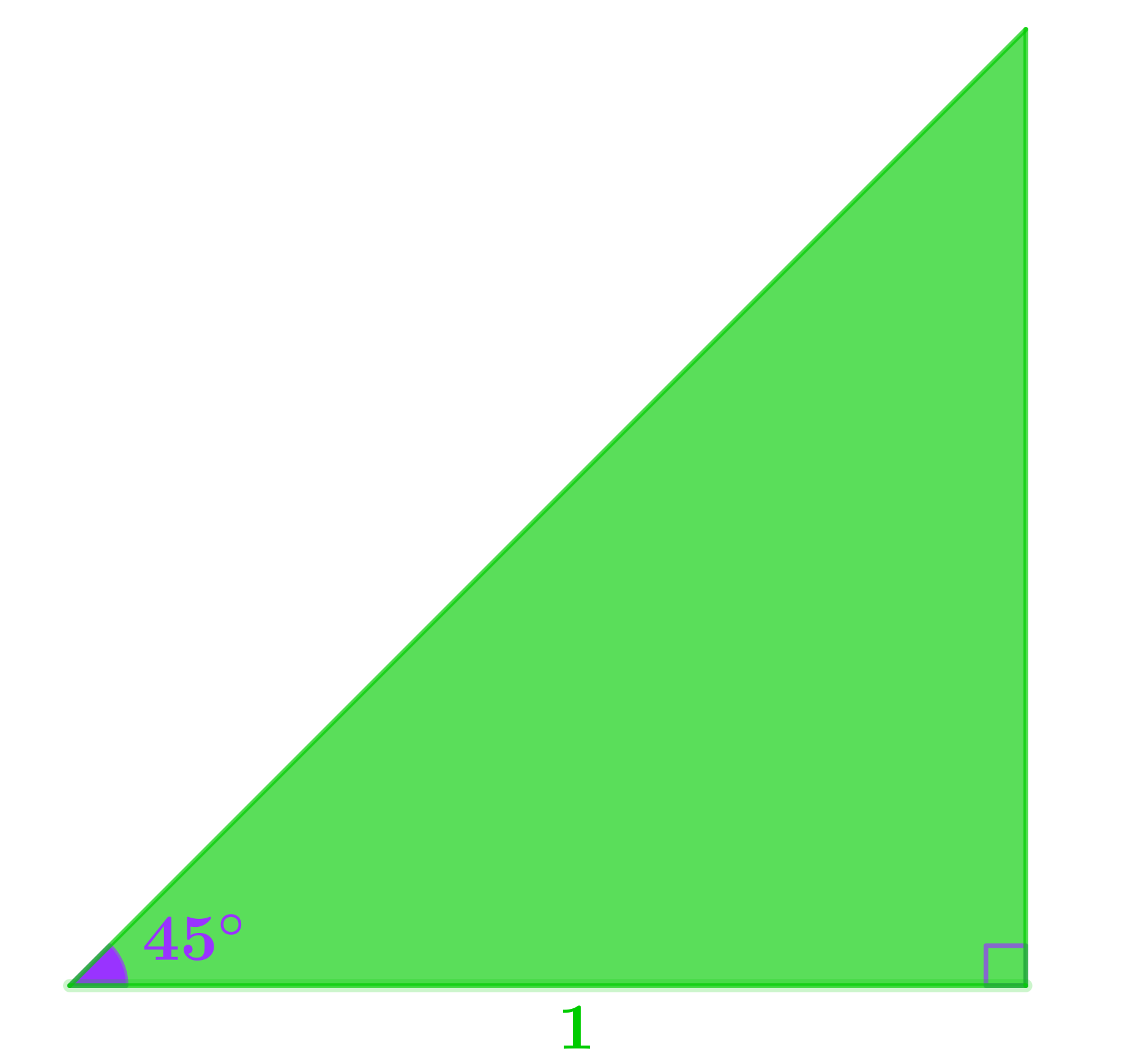
Here, your students will need to see that:
- the top angle is also \(45°\)
- the triangle is isosceles
- the vertical side of the triangle is also \(1\)
- they can use Pythagoras to find the hypotenuse
- they can use the trig ratios that they already know
- they can rationalise the denominator
These are all things that they can figure out for themselves, or at least by working with others: there is really no need for you to help at all!
Use this diagram to find sin, cos, and tan of \(45°\).
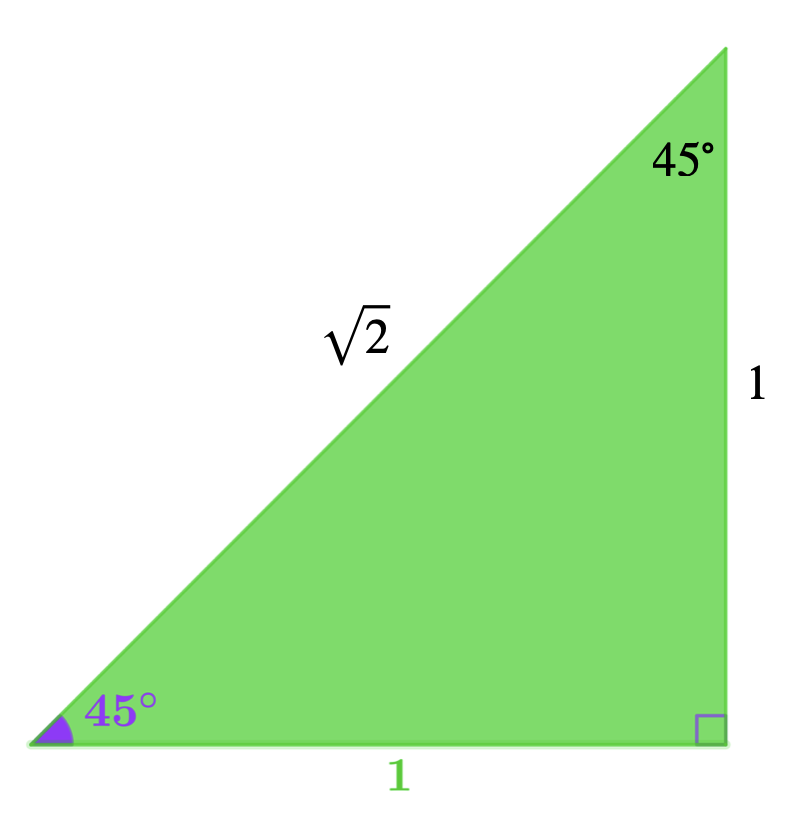
| \(\cos 45° = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}\) | \(\sin 45° = \dfrac{1}{\sqrt{2}} = \dfrac{\sqrt{2}}{2}\) | \(\tan 45° = 1\) |
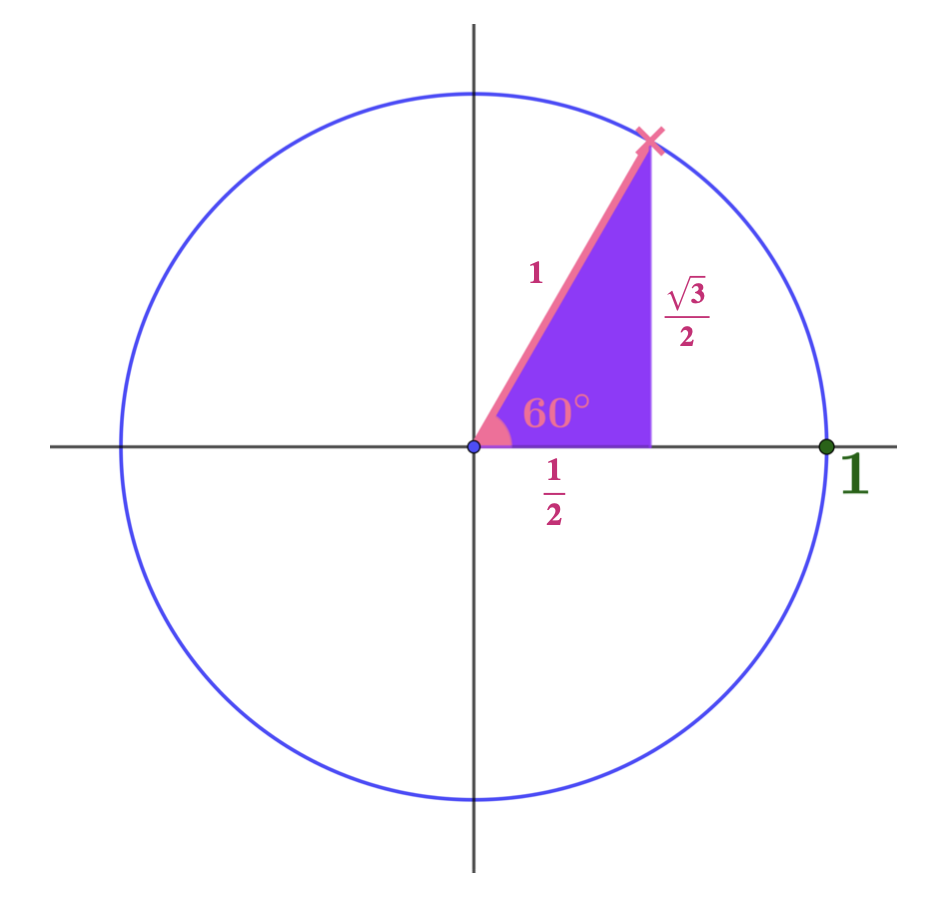
What are the coordinates of the pink point and the gradient of the pink radius?
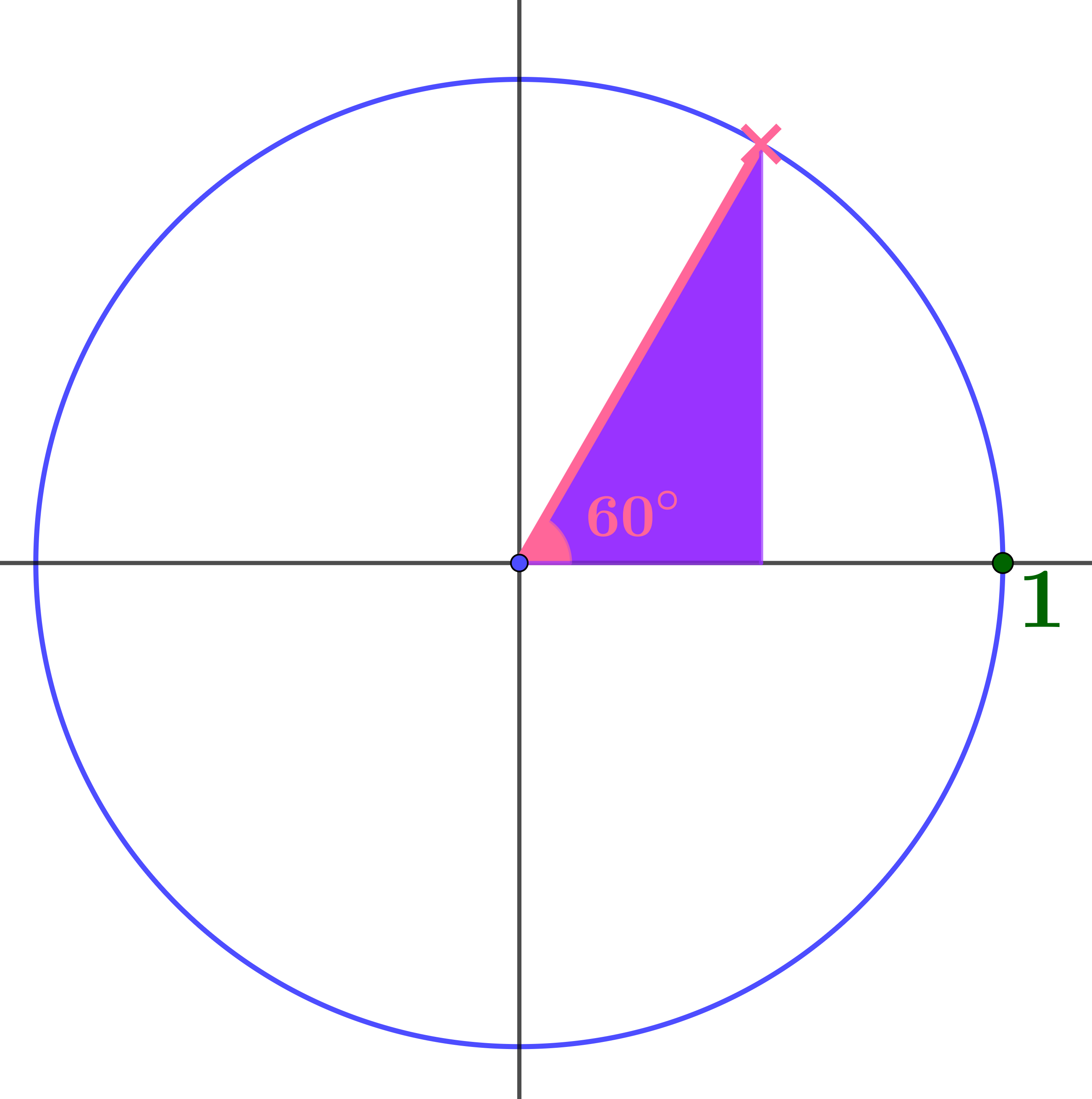
Putting what they have just done into the context of a unit circle is the first step towards generalising the trigonometric ratios in right-angled triangles to circular functions of any real number (whether or not that number corresponds to an angle). It might take a while before your students figure out that they are dealing with exactly the same problem as before, but they will, if given the time, the space, the encouragement, and the confidence to do so.
Some might have the coordinates and the gradient as \((\cos 60°, \sin 60°)\) and \(\tan 60°\), others as \(\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\) and \(\sqrt{3}\), but in discussion, it is really important to be sure that all your students understand both ways of writing the coordinates and gradient as this is the clue to extending the domains of the circular (trigonometric) functions.
What are the coordinates of the pink point and the gradient of the pink radius?
Now we can start thinking about new definitions of sin, cos, and tan. Our new definition of \(\cos 60^\circ\) is the \(x\) coordinate of the pink point; our new definition of \(\sin 60^\circ\) is the \(y\) coordinate of the pink point; and our new definition of \(\tan 60^\circ\) is the gradient of the pink radius.
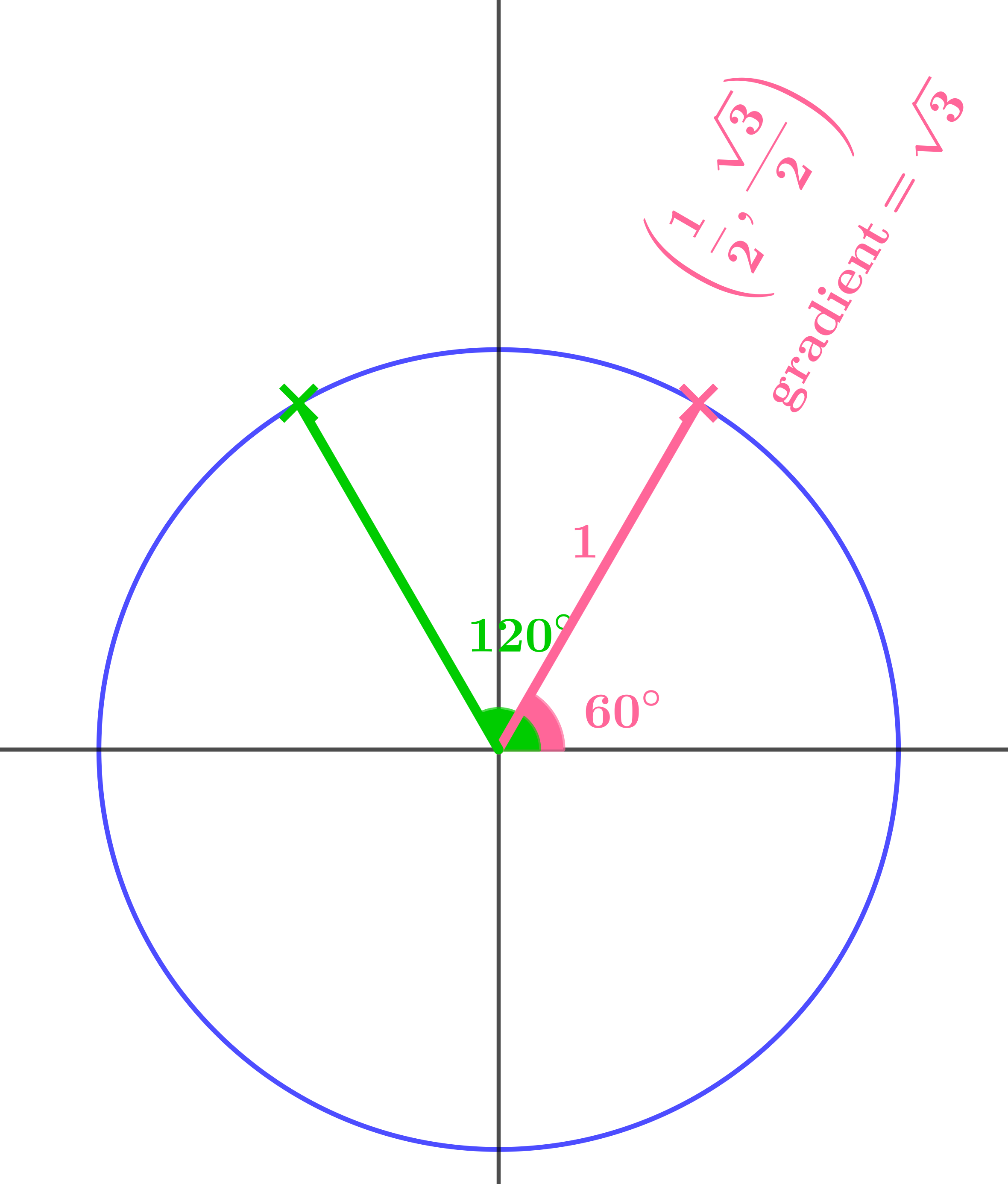
What are the coordinates of the green point and the gradient of the green radius?
Suggest values for sin, cos, and tan of \(120°\).
Again, resist the temptation to help by pointing out the symmetry and what this might mean for the coordinates and gradient. They can do this without you, and will benefit far more from doing so.
This is where they begin to see the relationship between coordinates and gradients on the one hand, and the circular functions sin, cos, and tan on the other.
The key word here is symmetry. It is the symmetry of the diagram that allows us to see right away that the coordinates of the green point are \(\left(-\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\) and that the gradient is \(-\sqrt{3}\).
The sequence of questions is designed to suggest that cos is the \(x\) coordinate, sin is the \(y\) coordinate, and tan is the gradient; suggest so strongly, in fact, that this conclusion appears more or less inevitable. What it achieves is giving students an idea of why this way of defining cos, sin, and tan agrees with their earlier understanding of the functions for angles between \(0°\) and \(90°\), and hence why assigning the value \(-\dfrac{1}{2}\) to \(\cos 120°\), for example, is reasonable.
Again, following your class discussion of this page, your students should have a diagram that has both the exact values of the coordinates and gradient, and the values in terms of cos, sin, and tan.
What are the coordinates of the green point and the gradient of the green radius?
Suggest values for sin, cos, and tan of \(120°\).
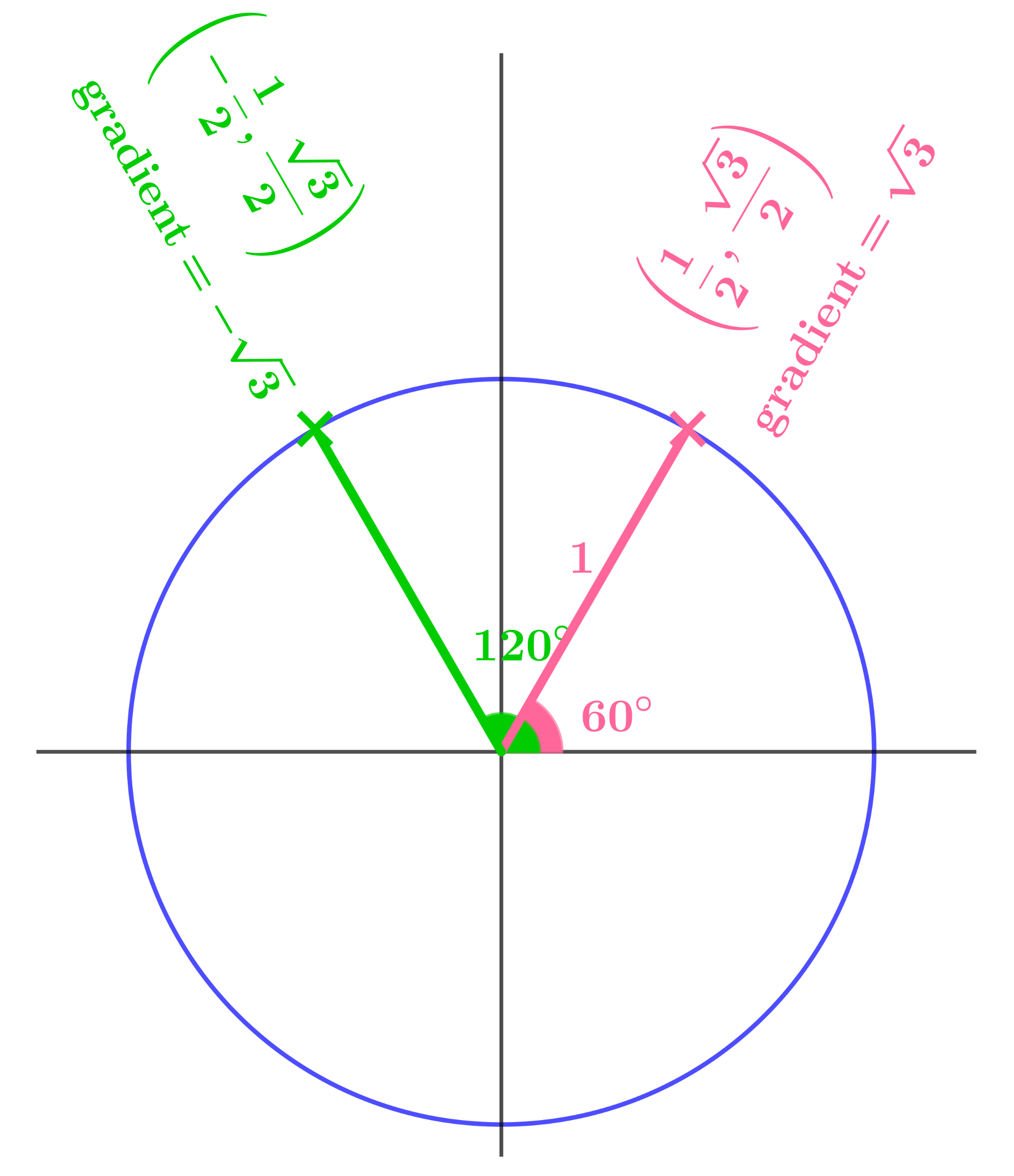
For the pink angle, cos is the \(x\) coordinate, sin is the \(y\) coordinate, and tan is the gradient. So the sensible option is to use the same definitions for the green angle to get:
| \(\cos 120° = -\dfrac{1}{2}\) | \(\sin 120° = \dfrac{\sqrt{3}}{2}\) | \(\tan 120° = -\sqrt{3}\) |
Suggest values for sin, cos, and tan of \(240°\) and \(300°\).
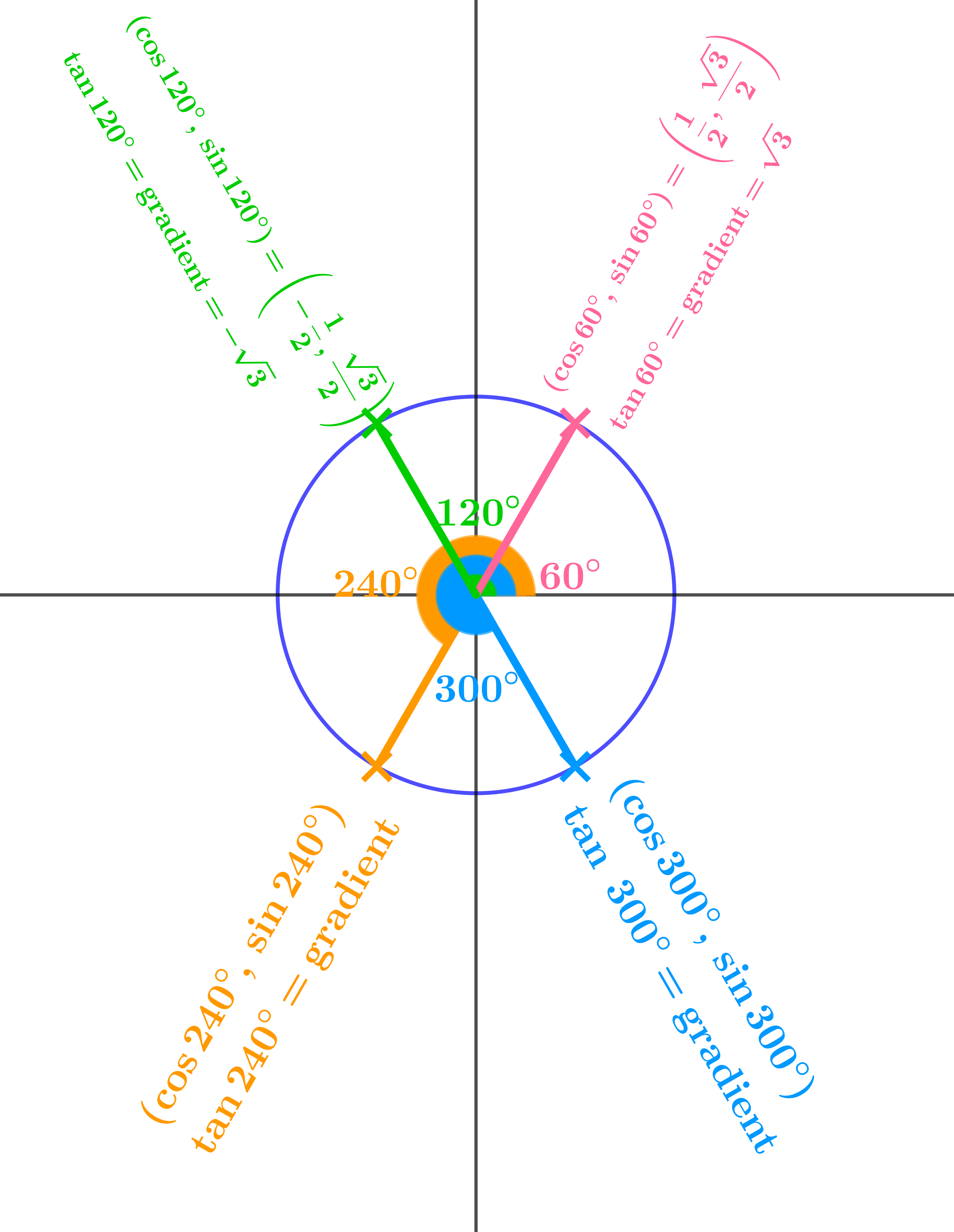
Suggest values for sin, cos, and tan of \(240°\) and \(300°\).
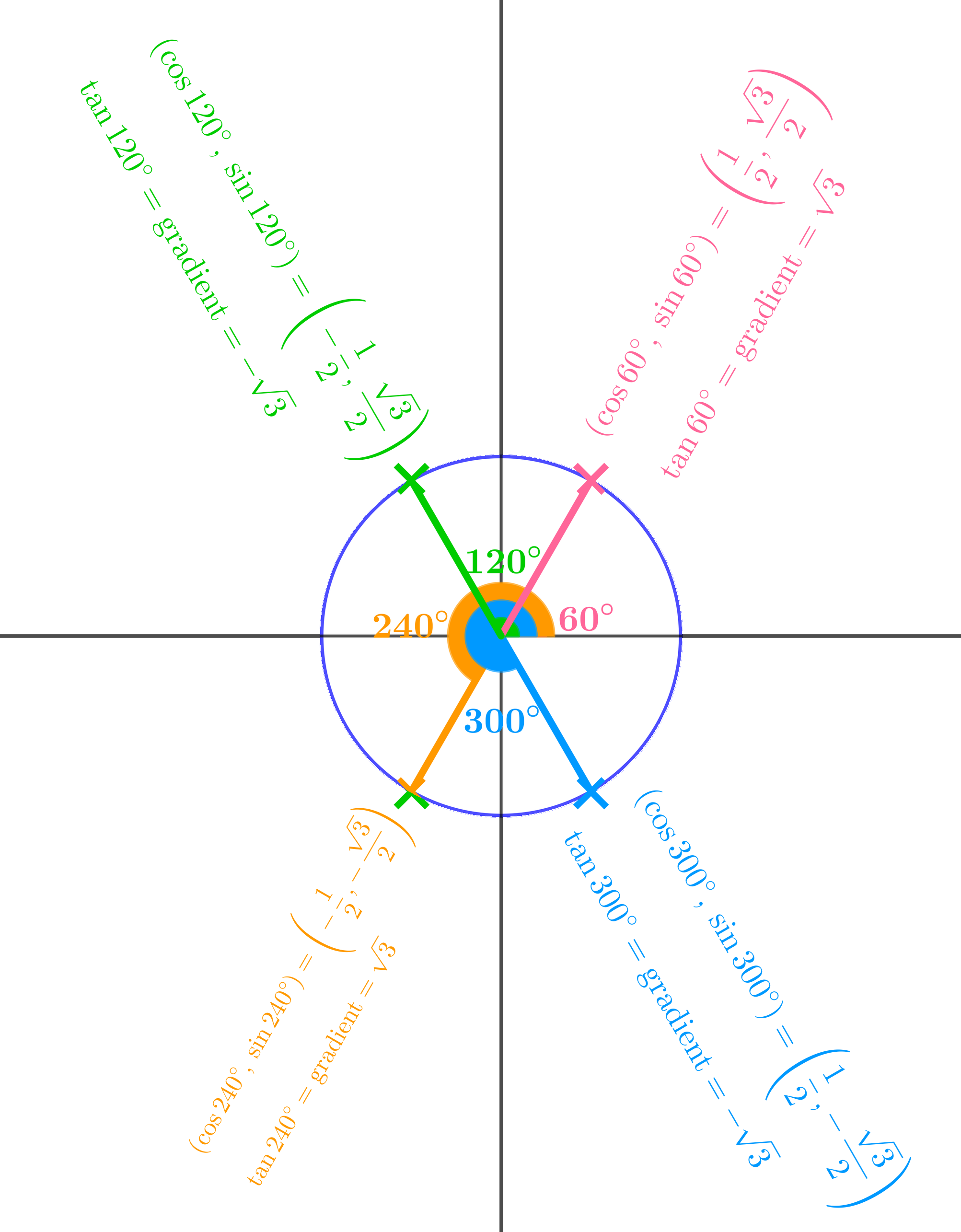
\[\begin{aligned} (\cos 240°, \sin 240°) = \left(-\dfrac{1}{2}, -\dfrac{\sqrt{3}}{2}\right),\quad &\text{gradient}= \tan 240° = \sqrt{3}\\[12pt] (\cos 300°, \sin 300°) = \left(\dfrac{1}{2}, -\dfrac{\sqrt{3}}{2}\right),\quad&\text{gradient}= \tan 300° = -\sqrt{3} \end{aligned} \]
Now we can build on this to extend our definitions to angles between \(0°\) and \(360°\), but your students have to figure out each step: what are the coordinates and gradients, and what are the angles, all using symmetry? This way, they become more familiar with the unit circle diagram and with its value for defining trigonometric functions.
This is probably a good moment to think about the name: trigon is a three-sided shape, and "metry" is to do with measurement, so "trigonometry" means "measurement of triangles". Here, however, we are trying to decouple the functions from the triangles, so the name "circular functions" makes far more sense. Consider introducing this new name for the functions at this point, though with an awareness that most resources will continue to use the term "trigonometric functions". I suppose we could justify this by understanding the term to mean "functions related to the measurement of triangles".
What are sin, cos, tan of \(420°\), \(780°\), \(1140°\), \(1500°\)?
This video should help.
What about angles bigger than \(360°\) and negative angles?
These are strange ideas: how can an angle be negative, and how can an angle be bigger than \(360°\)? The answer is that they can't really, so here we are beginning to uncouple the functions from the idea of angles altogether. Ultimately, this will lead to definitions that have nothing to do with triangles or circles, and graphs will become more useful as tools for thinking about them. For now, though, we can extend our ideas of angles to include these strange animals using the unit circle.
Here, students are led to the extension of the circular functions to these "non-existent" angles just as they were at the start to angles bigger than right-angles.
Each of these "angles" has the same sin, cos, and tan as \(60°\).
What are sin, cos, tan of \(420°\), \(780°\), \(1140°\), \(1500°\)?
They are all \(60^\circ+\) multiples of \(360^\circ\), so sin, cos, and tan are all the same as sin, cos, tan of \(60°\).
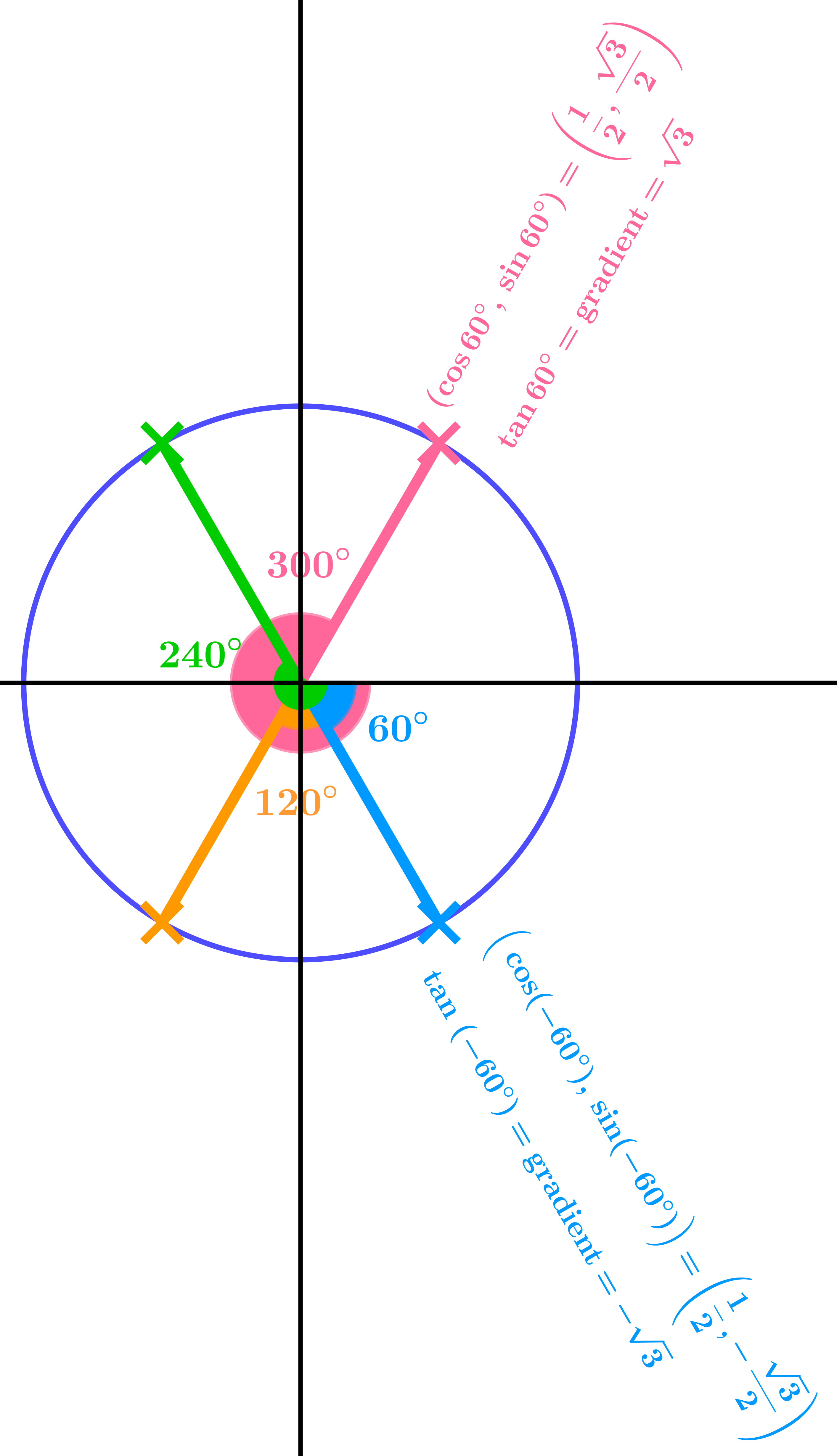
Suggest values for sin, cos, tan of \(-60°\).
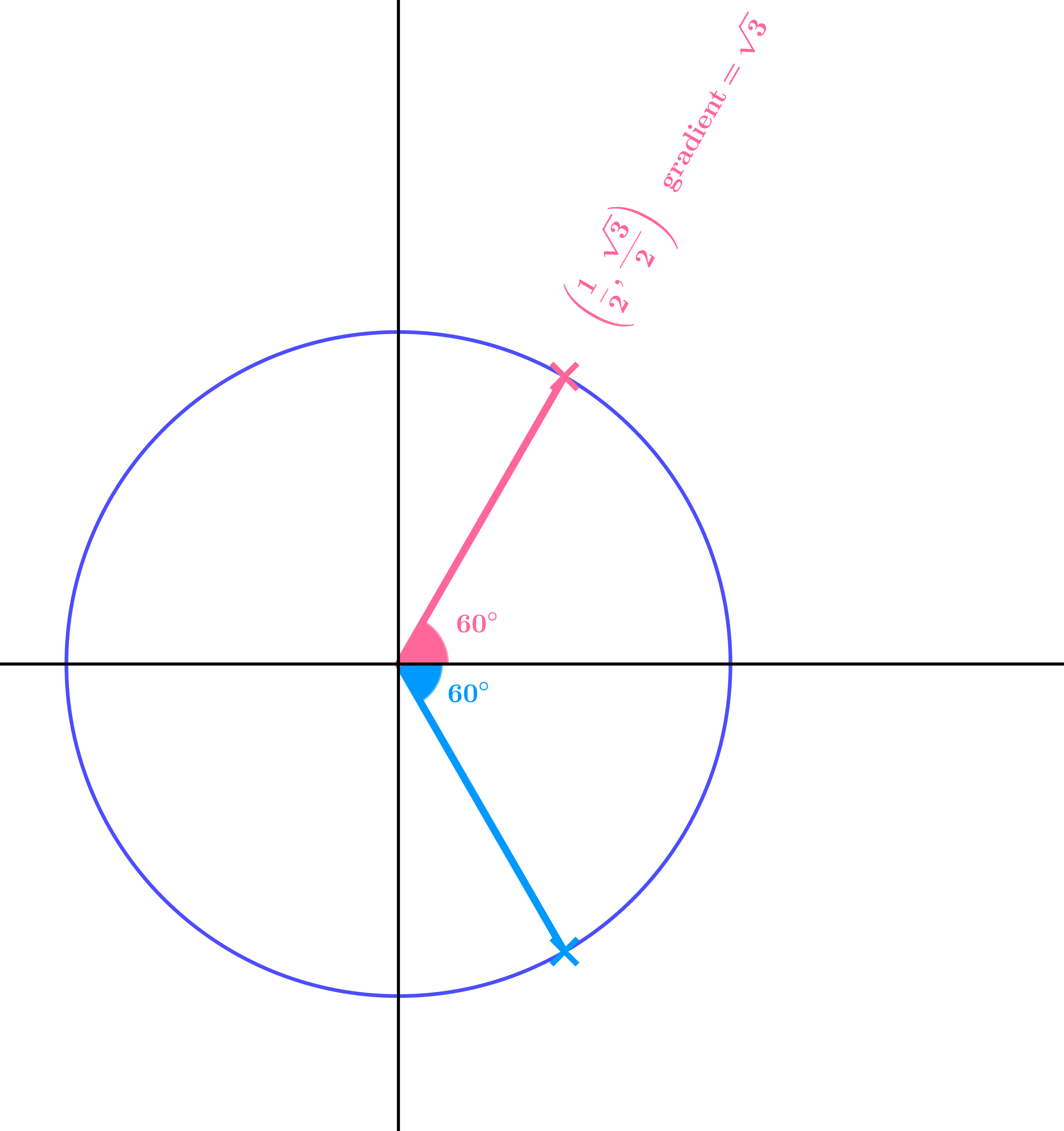
Suggest values for sin, cos, tan of \(-60°\).
Angles are measured from the positive \(x\) axis in the anticlockwise direction, so it makes sense to count angles measured in the clockwise direction as negative. From the geometrical point of view, the angle size is still positive, but from the functional point of view, the angle counts as a negative.
| \(\cos(-60°) = \dfrac{1}{2}\) | \(\sin(-60°) = -\dfrac{\sqrt{3}}{2}\) | \(\tan(-60°) = -\sqrt{3}\) |
Suggest values for sin, cos, tan of \(-120°\), \(-240°\), \(-300°\).
So far, all angles have been measured anticlockwise from the positive \(x\) axis. This has been so obvious from the start that it may well not even have been mentioned up to this point.
The time has come to make this more explicit and to discuss the appropriateness of using angles measured clockwise from the positive \(x\) axis as representative of negative angles.
This always raises the question of labelling on the diagram: should we label the blue angle here \(60°\) or \(-60°\)? There is no hard and fast rule here. I prefer to label the diagram with a positive number, because, for example here, the angle really is \(60°\) in the sense that your students have always understood it. But then I use \(-60°\) in my working.
Suggest values for sin, cos, tan of \(-120°\), \(-240°\), \(-300°\).

Suggest values for sin, cos, tan of \(-120°\), \(-240°\), \(-300°\).
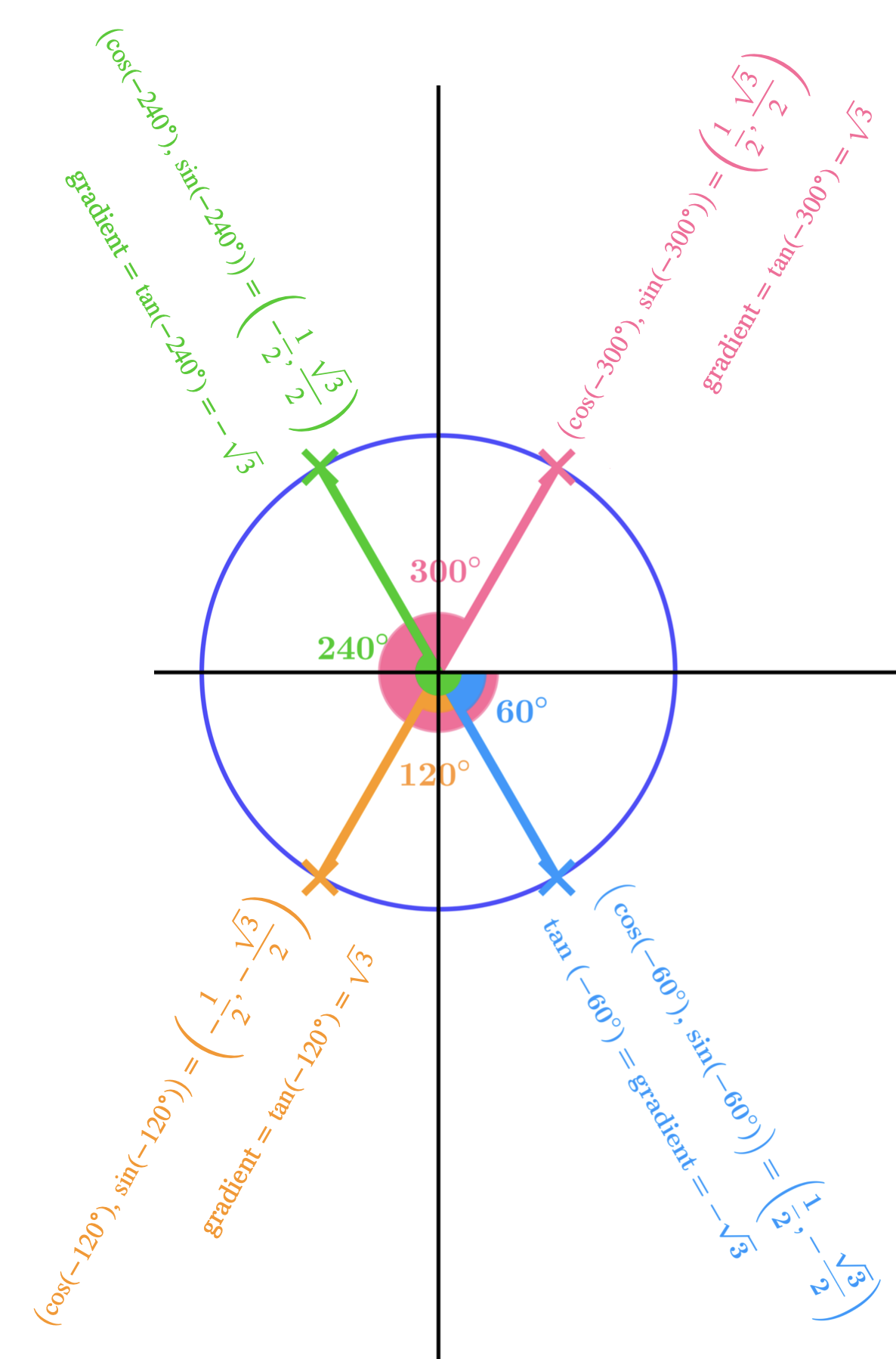
| \(\cos(-60°) = \dfrac{1}{2}\) | \(\sin(-60°) = -\dfrac{\sqrt{3}}{2}\) | \(\tan(-60°) = -\sqrt{3}\) |
| \(\cos(-120°) = -\dfrac{1}{2}\) | \(\sin(-120°) = -\dfrac{\sqrt{3}}{2}\) | \(\tan(-120°) = \sqrt{3}\) |
| \(\cos(-240°) = -\dfrac{1}{2}\) | \(\sin(-240°) = \dfrac{\sqrt{3}}{2}\) | \(\tan(-240°) = -\sqrt{3}\) |
| \(\cos(-300°) = \dfrac{1}{2}\) | \(\sin(-300°) = \dfrac{\sqrt{3}}{2}\) | \(\tan(-300°) = \sqrt{3}\) |
Suggest values for sin, cos, tan of \(-660°\), \(-1020°\), \(-1380°\), \(-1740°\).
Each of these "angles" has the same sin, cos, and tan as \(-300°\).
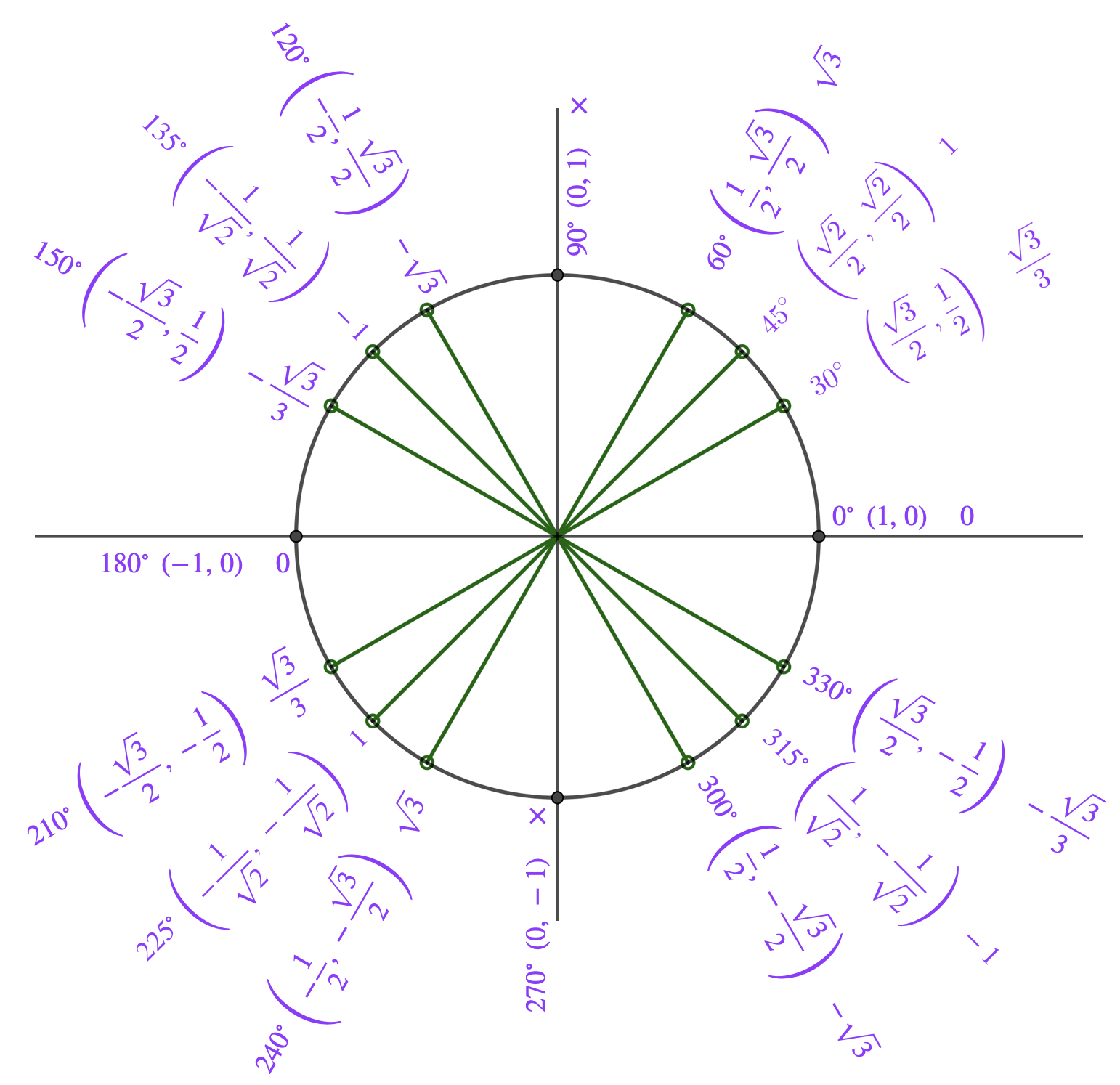
These diagrams essentially form definitions of sin, cos, and tan of any number (angle).
There are other ways to define these functions using, for example, graphs or power series, but this one makes intuitive sense and forms a reliable foundation for what is to come.
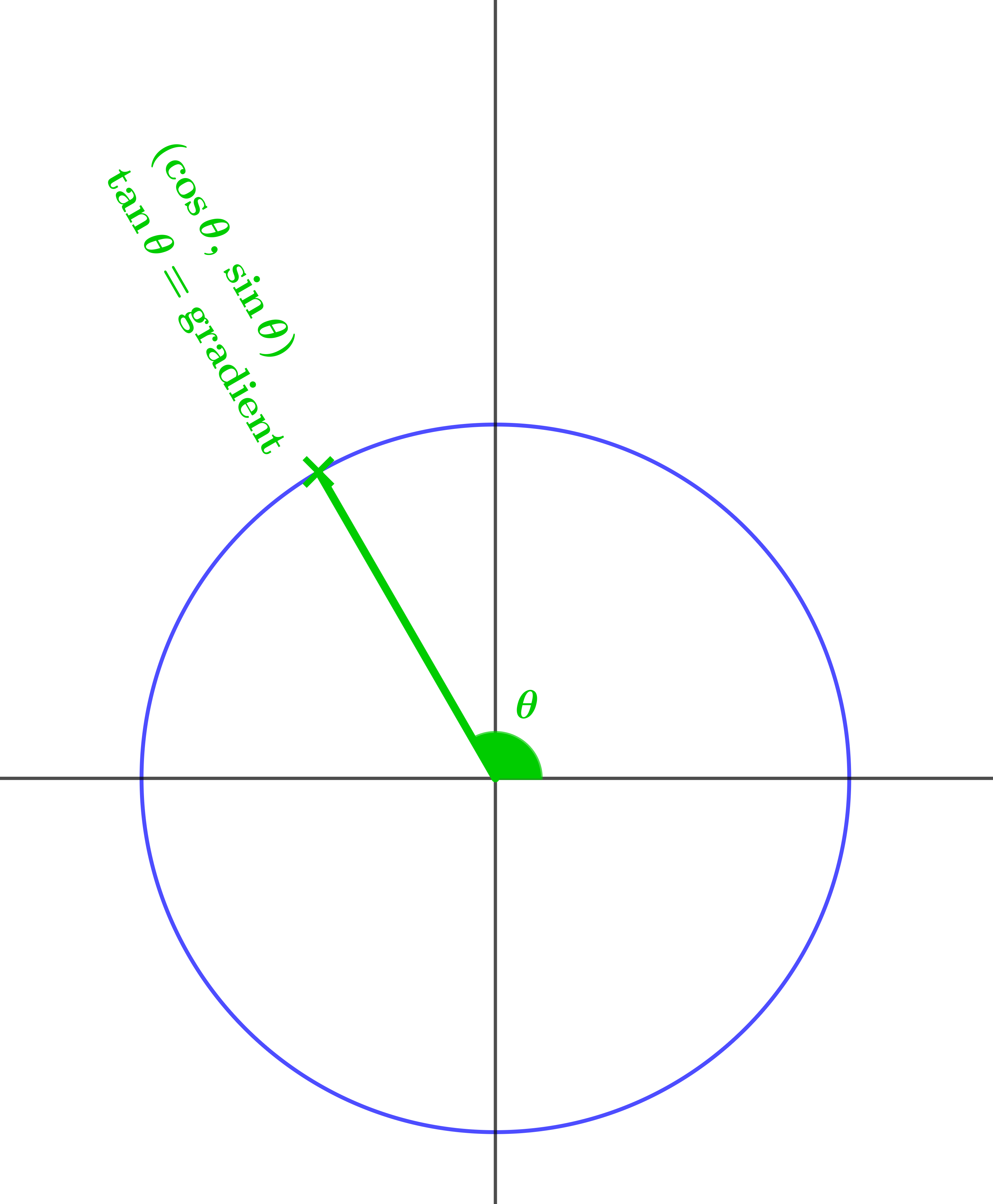
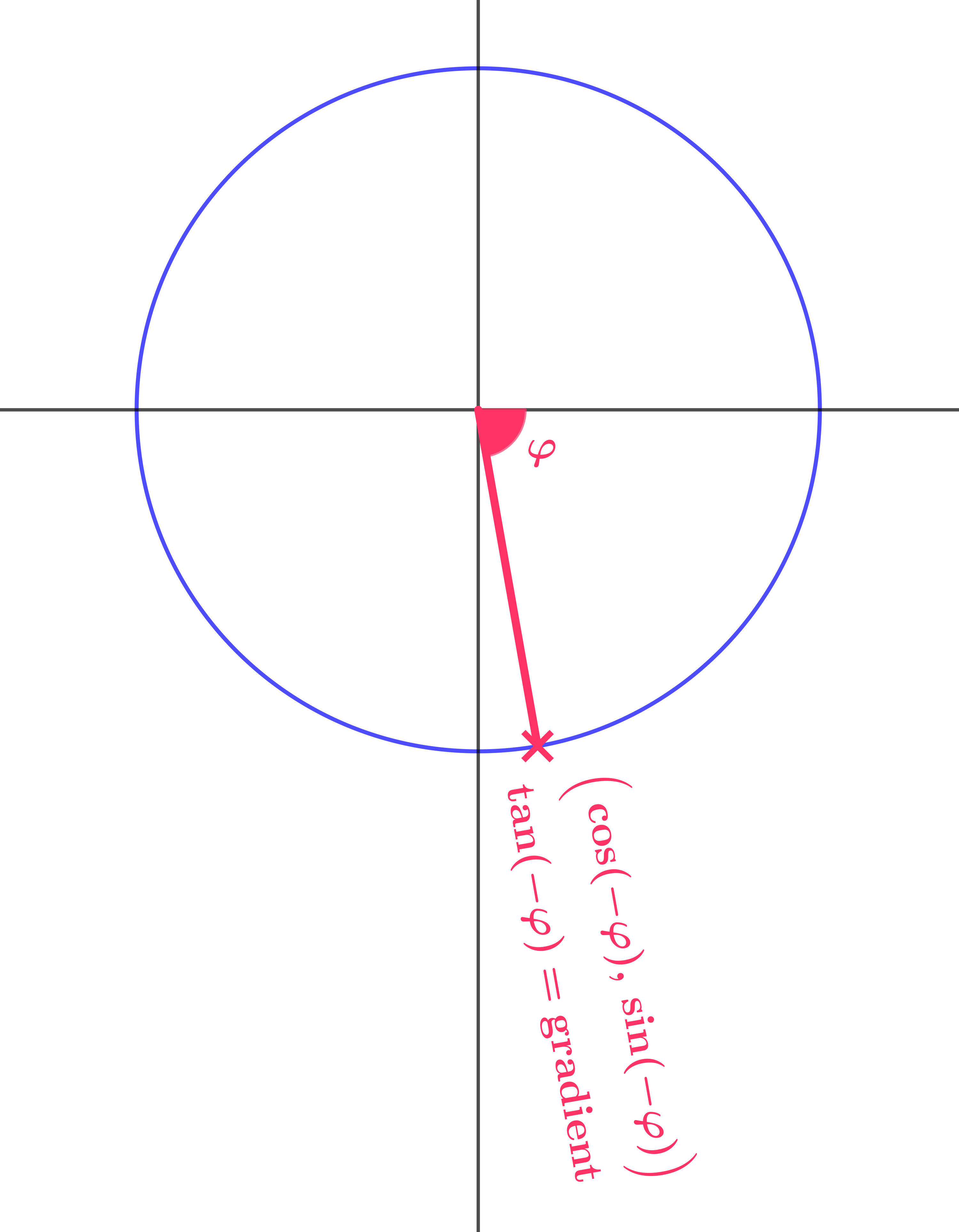
Complete this diagram.
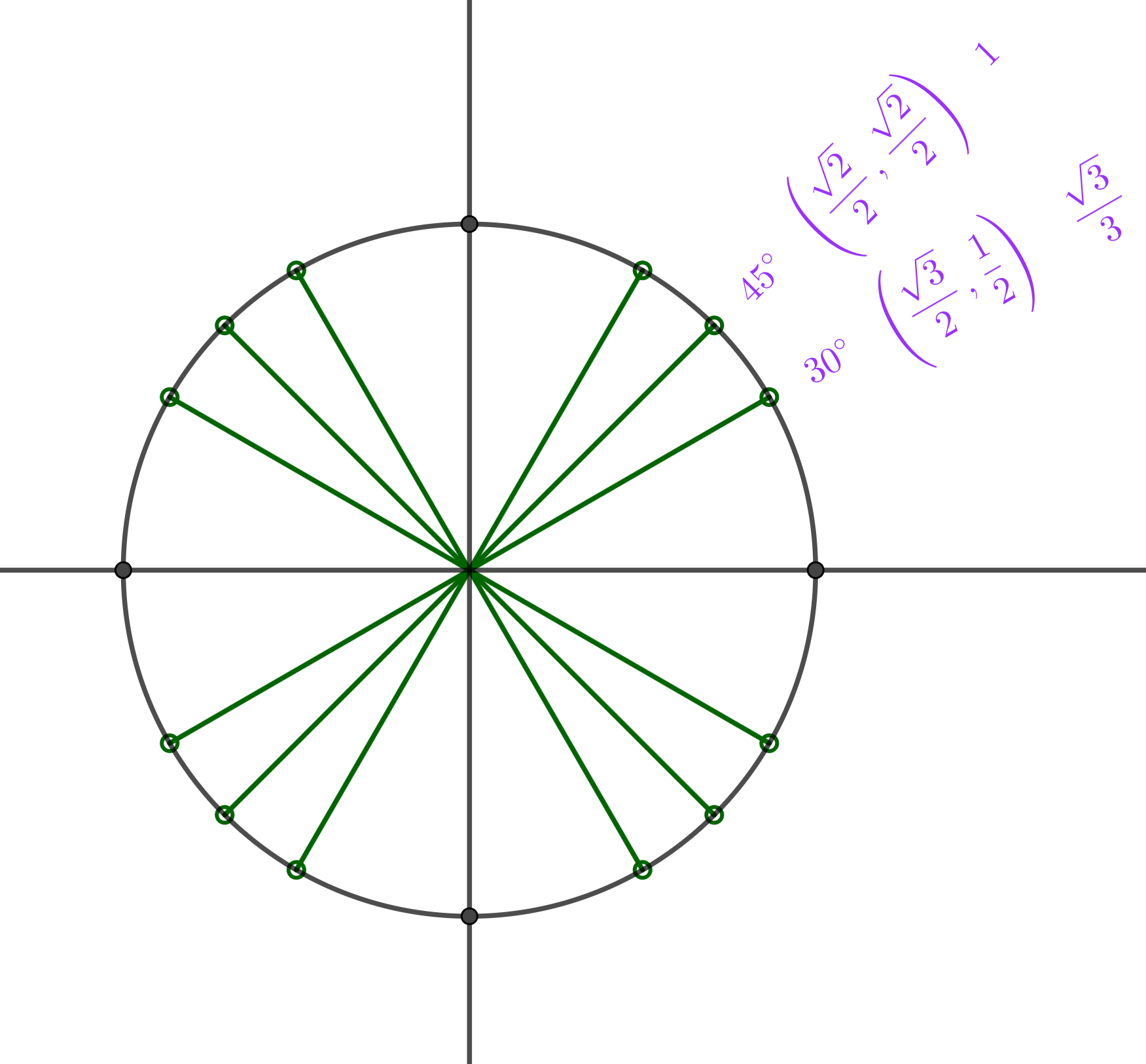
This diagram is absolutely fundamental to all understanding of the circular functions, and I want my students to know it intimately. To this end, I ask them to fill in a blank copy at the start of several lessons; I even set a timing goal. If they can do this fluently, they have a really strong understanding of what the circular functions are all about.
It's handy to know these without the calculator, but ultimately, knowing this diagram is about insight, not about practicality. Every time you use a calculator for one of these, you erode your understanding of the meaning of the circular functions.

Congratulations on completing the first stage!
You've now explored the foundations of circular functions and seen how they extend beyond the trigonometry of right-angled triangles. By understanding the unit circle and working through these definitions, you've built a solid foundation for everything that follows.
Keep practising that unit circle diagram—it's the key to mastering circular functions!